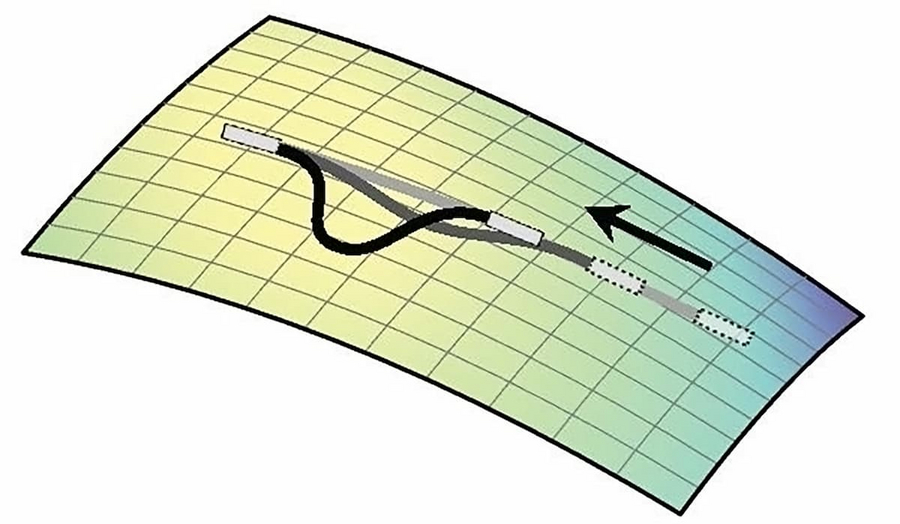
An elastic line confined to a curved surface buckles and bends under increasing compression (arrow). © Shiheng Zhao and Pierre A. Haas / MPIPKS / MPI-CBG
A straight metal bar bends under sufficiently high compression because the energetic cost of bending the bar drops below that of compressing the straight bar further. This buckling is an example of a mechanical instability.
Nearly three centuries ago, a Swiss mathematician, Leonhard Euler, laid the mathematical foundations for describing such instabilities by explaining the buckling of an elastic line at a critical value of the compressive force. Centuries of work by other mathematicians and scientists built upon Euler’s ideas to describe more complex buckling instabilities. One seemingly innocuous question remained open, though: How does a compressed line buckle within a curved surface?
Pierre Haas, research group leader at the Max Planck Institute for the Physics of Complex Systems (MPIPKS), the Max Planck Institute of Molecular Cell Biology and Genetics (MPI-CBG), and the Center for Systems Biology Dresden (CSBD), and Shiheng Zhao, doctoral student in the group of Pierre Haas, have now answered this question that Euler did not solve: Combining exact and numerical calculations, the researchers discovered that the mathematical structure of the mechanical instability changes fundamentally within a curved surface.
“We found that buckling happens differently if the line is constrained to a curved surface: the critical force for the instability is zero, so the line starts bending even at small compressive forces. However, as we keep compressing the line, it snaps suddenly to a higher compression and bends even more,” says Shiheng Zhao.
These theoretical results are the foundations explaining a class of elastic instabilities within curved surfaces that also has biological relevance. Shiheng Zhao and Pierre Haas, together with colleagues from Princeton and the Flatiron Institute, have recently shown that the morphogenesis of the hindgut of the fruit fly Drosophila can be explained by an analogous mechanical instability within a curved surface.
While buckling instabilities are classical marks of material failure in engineering applications, this and related mechanical instabilities have only been recognized more recently as an important mechanism for the emergence of shape in developmental biology. “Our findings can help us understand how tissues composed of many cells develop into organs and organisms, because the mechanical forces that drive development often act on curved, rather than flat, tissues,” Pierre Haas therefore concludes.
Shiheng Zhao (赵世恒) and Pierre A. Haas: Euler Buckling on Curved Surfaces. Phys. Rev. Lett. 135, 247201 – Published 10 December, 2025, doi: 10.1103/63py-ph5s.