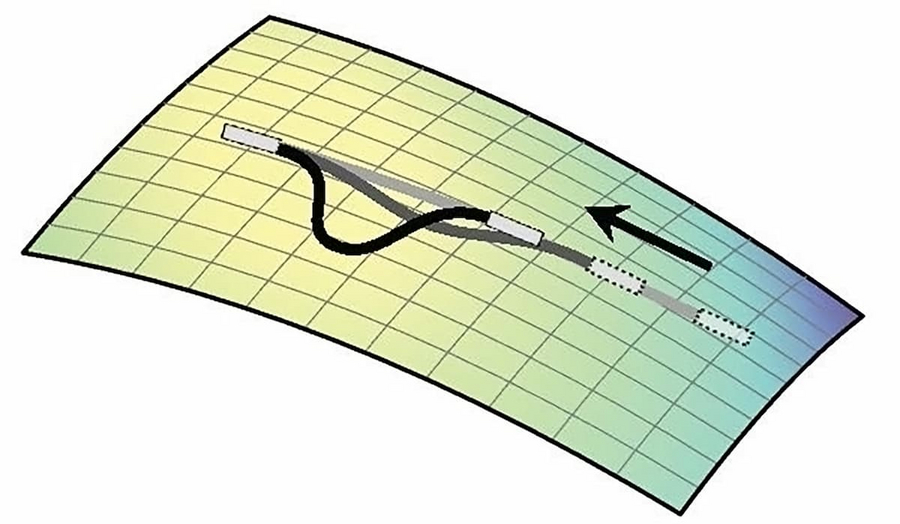
Eine elastische Linie in einer gekrümmten Fläche knickt und verbiegt sich unter zunehmender Kompression (Pfeil). © Shiheng Zhao and Pierre A. Haas / MPIPKS / MPI-CBG
Eine gerade Metallstange verbiegt sich unter ausreichend hoher Kompression, da die energetischen Kosten für das Verbiegen der Stange geringer werden als die für das weitere Zusammendrücken der geraden Stange. Dieses Knicken ist ein Beispiel einer mechanischen Instabilität.
Vor fast drei Jahrhunderten legte der Schweizer Mathematiker Leonhard Euler die mathematischen Grundlagen für diese Instabilitäten, indem er die Knickung einer elastischen Linie bei einem kritischen Wert der Druckkraft erklärte. Auf Eulers Ideen bauten andere Mathematiker und Wissenschaftler über Jahrhunderte hinweg auf, um komplexere Knickinstabilitäten zu beschreiben. Eine scheinbar banale Frage blieb jedoch offen: Wie knickt eine zusammengedrückte Linie in einer gekrümmten Fläche?
Pierre Haas, Forschungsgruppenleiter am Max-Planck-Institut für Physik komplexer Systeme (MPIPKS), am Max-Planck-Institut für molekulare Zellbiologie und Genetik (MPI-CBG) und am Zentrum für Systembiologie Dresden (CSBD) und Shiheng Zhao, Doktorand in der Gruppe von Pierre Haas, haben nun diese von Euler ungelöste Frage beantwortet: Durch die Kombination exakter und numerischer Berechnungen entdeckten die Forscher, dass sich die mathematische Struktur der mechanischen Instabilität in einer gekrümmten Fläche grundlegend verändert.
Diese theoretischen Ergebnisse bilden die Grundlage für die Erklärung einer Klasse elastischer Instabilitäten in gekrümmten Flächen, die auch biologische Relevanz haben. Zusammen mit Kolleginnen und Kollegen aus Princeton und dem Flatiron Institute haben Shiheng Zhao und Pierre Haas kürzlich gezeigt, dass die Morphogenese des Hinterdarms der Fruchtfliege Drosophila durch eine ähnliche mechanische Instabilität in einer gekrümmten Fläche erklärt werden kann.
Während Knickinstabilitäten klassische Anzeichen für Materialversagen in ingenieurtechnischen Anwendungen sind, sind diese und ähnliche mechanische Instabilitäten erst in jüngerer Zeit als wichtiger Mechanismus der Formentstehung in der Entwicklungsbiologie erkannt worden. „Unsere Ergebnisse können dabei helfen zu verstehen, wie sich aus vielen Zellen bestehende Gewebe zu Organen und Organismen entwickeln, da die mechanischen Kräfte, die deren Entwicklung vorantreiben, oft auf gekrümmte und nicht auf flache Gewebe wirken“, fasst Pierre Haas zusammen.
Shiheng Zhao (赵世恒) and Pierre A. Haas: Euler Buckling on Curved Surfaces. Phys. Rev. Lett. 135, 247201 – Published 10 December, 2025, doi: 10.1103/63py-ph5s.