We are mathematicians working at the interface of mathematics and science. Our research focuses on developing mathematics and methods to tackle challenges in current biology and living systems. Our work builds on a number of mathematical disciplines such as computational mathematics, applied algebraic geometry and algebraic topology, statistics, optimization, machine learning, network theory, and systems biology.
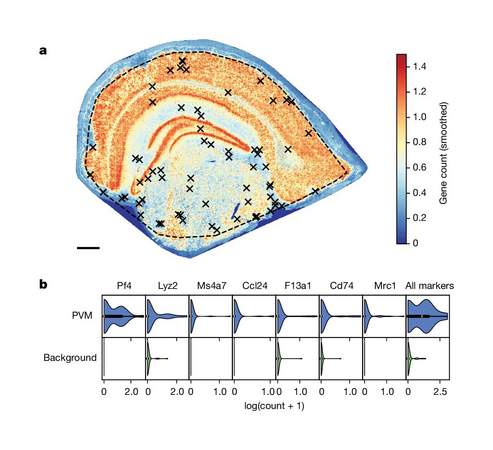
Spatial transcriptomics measures in situ gene expression at millions of locations within a tissue1, hitherto with some trade-off between transcriptome depth, spatial resolution and sample size. Although integration of image-based segmentation has enabled impactful work in this context, it is limited by imaging quality and tissue heterogeneity. By contrast, recent array-based technologies offer the ability to measure the entire transcriptome at subcellular resolution across large samples. Presently, there exist no approaches for cell type identification that directly leverage this information to annotate individual cells. Here we propose a multiscale approach to automatically classify cell types at this subcellular level, using both transcriptomic information and spatial context. We showcase this on both targeted and whole-transcriptome spatial platforms, improving cell classification and morphology for human kidney tissue and pinpointing individual sparsely distributed renal mouse immune cells without reliance on image data. By integrating these predictions into a topological pipeline based on multiparameter persistent homology we identify cell spatial relationships characteristic of a mouse model of lupus nephritis, which we validate experimentally by immunofluorescence. The proposed framework readily generalizes to new platforms, providing a comprehensive pipeline bridging different levels of biological organization from genes through to tissues.
Benjamin, K., Bhandari, A., Kepple, J.D. et al. Multiscale topology classifies cells in subcellular spatial transcriptomics. Nature 630, 943–949 (2024). doi.org/10.1038/s41586-024-07563-1
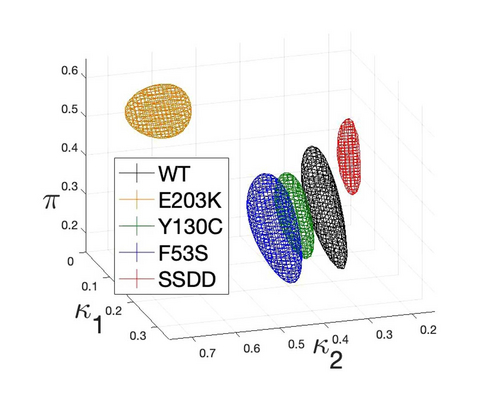
The MEK/ERK signalling pathway is involved in cell division, cell specialisation, survival and cell death. Here we study a polynomial dynamical system describing the dynamics of MEK/ERK proposed by Yeung et al. with their experimental setup, data and known biological information. The experimental dataset is a time-course of ERK measurements in different phosphorylation states following activation of either wild-type MEK or MEK mutations associated with cancer or developmental defects. We demonstrate how methods from computational algebraic geometry, differential algebra, Bayesian statistics and computational algebraic topology can inform the model reduction, identification and parameter inference of MEK variants, respectively. Throughout, we show how this algebraic viewpoint offers a rigorous and systematic analysis of such models.
Marsh, L., Dufresne, E., Byrne, H., & Harrington, H. A. (2022). Algebra, Geometry and Topology of ERK Kinetics. Bulletin of Mathematical Biology, 84, Article 137. Advance online publication. https://doi.org/10.1007/s11538-022-01088-2
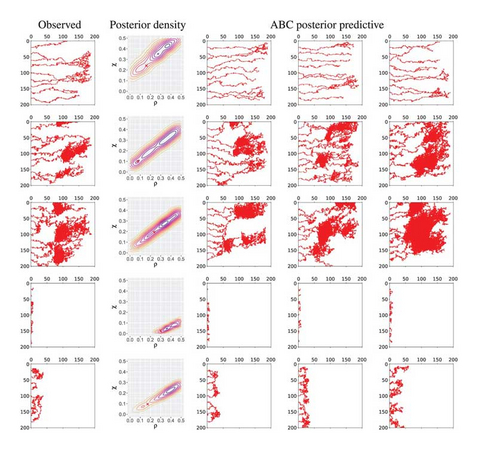
Inferring the parameters of models describing biological systems is an important problem in the reverse engineering of the mechanisms underlying these systems. Much work has focused on parameter inference of stochastic and ordinary differential equation models using Approximate Bayesian Computation (ABC). While there is some recent work on inference in spatial models, this remains an open problem. Simultaneously, advances in topological data analysis (TDA), a field of computational mathematics, have enabled spatial patterns in data to be characterized. Here, we focus on recent work using TDA to study different regimes of parameter space for a well-studied model of angiogenesis. We propose a method for combining TDA with ABC to infer parameters in the Anderson–Chaplain model of angiogenesis. We demonstrate that this topological approach outperforms ABC approaches that use simpler statistics based on spatial features of the data. This is a first step toward a general framework of spatial parameter inference for biological systems, for which there may be a variety of filtrations, vectorizations and summary statistics to be considered.
Thomas Thorne, Paul D W Kirk, Heather A Harrington, Topological approximate Bayesian computation for parameter inference of an angiogenesis model, Bioinformatics, Volume 38, Issue 9, March 2022, Pages 2529–2535, https://doi.org/10.1093/bioinformatics/btac118
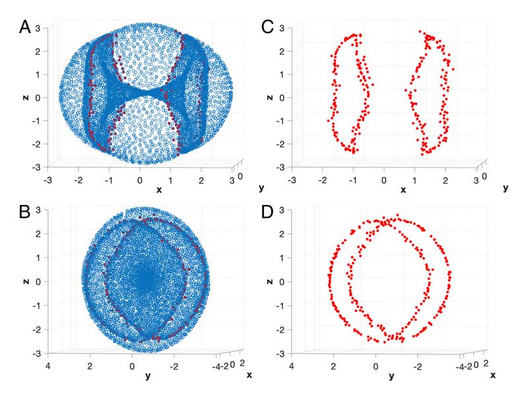
The quest for low-dimensional models which approximate high-dimensional data is pervasive across the physical, natural, and social sciences. The dominant paradigm underlying most standard modeling techniques assumes that the data are concentrated near a single unknown manifold of relatively small intrinsic dimension. Here, we present a systematic framework for detecting interfaces and related anomalies in data which may fail to satisfy the manifold hypothesis. By computing the local topology of small regions around each data point, we are able to partition a given dataset into disjoint classes, each of which can be individually approximated by a single manifold. Since these manifolds may have different intrinsic dimensions, local topology discovers singular regions in data even when none of the points have been sampled precisely from the singularities. We showcase this method by identifying the intersection of two surfaces in the 24-dimensional space of cyclo-octane conformations and by locating all of the self-intersections of a Henneberg minimal surface immersed in 3-dimensional space. Due to the local nature of the topological computations, the algorithmic burden of performing such data stratification is readily distributable across several processors.
Bernadette J. Stolz, Jared Tanner, Heather A. Harrington, and Vidit Nanda. Geometric anomaly detection in data. August 3, 2020, 117 (33) 19664-19669, https://doi.org/10.1073/pnas.2001741117
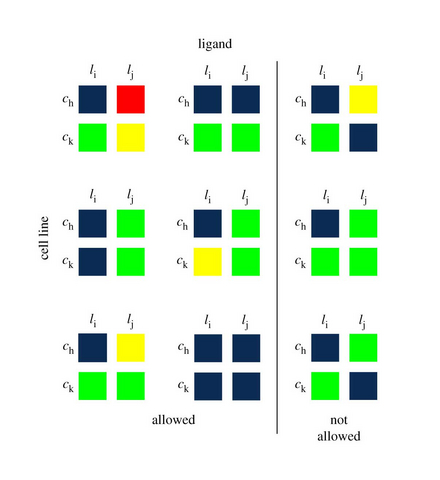
We introduce a tensor-based clustering method to extract sparse, low-dimensional structure from high-dimensional, multi-indexed datasets. This framework is designed to enable detection of clusters of data in the presence of structural requirements which we encode as algebraic constraints in a linear program. Our clustering method is general and can be tailored to a variety of applications in science and industry. We illustrate our method on a collection of experiments measuring the response of genetically diverse breast cancer cell lines to an array of ligands. Each experiment consists of a cell line–ligand combination, and contains time-course measurements of the early signalling kinases MAPK and AKT at two different ligand dose levels. By imposing appropriate structural constraints and respecting the multi-indexed structure of the data, the analysis of clusters can be optimized for biological interpretation and therapeutic understanding. We then perform a systematic, large-scale exploration of mechanistic models of MAPK–AKT crosstalk for each cluster. This analysis allows us to quantify the heterogeneity of breast cancer cell subtypes, and leads to hypotheses about the signalling mechanisms that mediate the response of the cell lines to ligands.
Seigal A, Beguerisse-Díaz M, Schoeberl B, Niepel M, Harrington HA. Tensor clustering with algebraic constraints gives interpretable groups of crosstalk mechanisms in breast cancer. J R Soc Interface. 2019 Feb 28;16(151):20180661. doi: 10.1098/rsif.2018.0661. PMID: 30958184; PMCID: PMC6408352.
