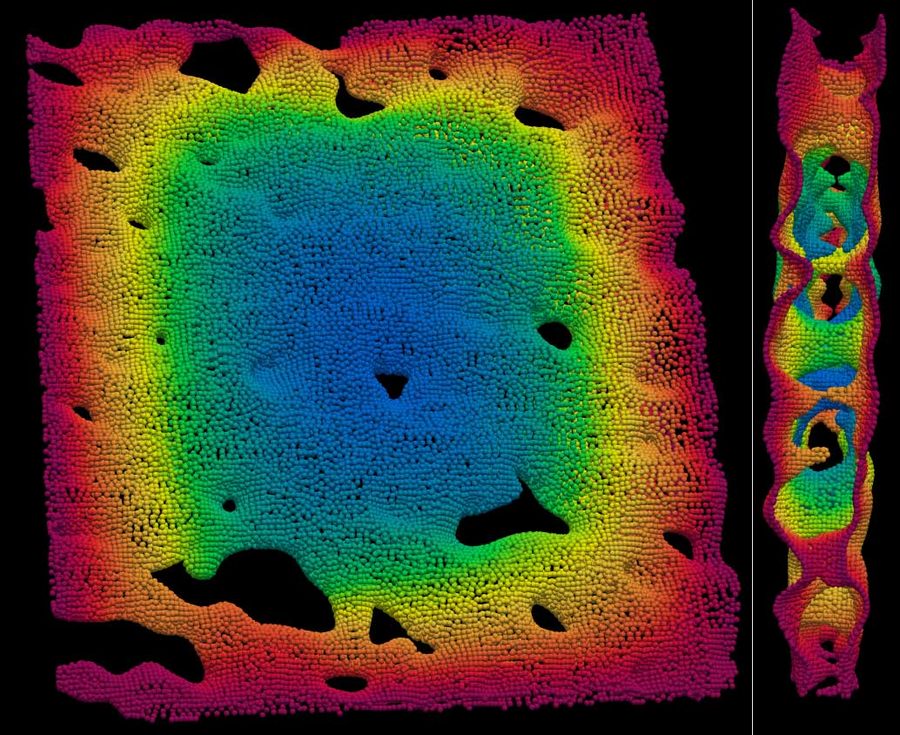
Fluorescence recovery after photobleaching simulation of a membrane protein in the endoplasmic reticulum. © Abhinav Singh / MPI-CBG
Biophysical processes occurring on curved surfaces, such as the diffusion of proteins in an organelle's membrane, have always been a significant challenge for computational models. Traditional approaches to such phenomena use flatness assumptions to simplify the modeling and predict the phenomenology. This is primarily done because solving differential-equation models on curved surfaces is challenging and computationally intensive. However, cell parts aren't usually flat; they're curved. To really understand the complexity of spatiotemporal dynamics on curved surfaces, we need accurate computational methods. For example, imagine trying to observe how a membrane protein moves on a bumpy part of a cell from microscopy videos of the fluorescently labeled protein. If we pretend the bumpy part is flat, our answers won't be very accurate. We need to use better methods to capture the role of shape.
In a recent study published in the Journal of Scientific Computing, the research group of Ivo Sbalzarini, TU Dresden Professor at the Center for Systems Biology Dresden (CSBD), Research Group Leader at the Max Planck Institute of Molecular Cell Biology and Genetics (MPI-CBG), and Dean of the Faculty of Computer Science at TU Dresden, has developed an innovative scalable algorithm that allows biophysical models to accurately respect the curvature and shape of a surface. This simplifies simulating cellular phenomena on curved membranes without trading off accuracy.
The first author of the study, Abhinav Singh, explains: “This new algorithm simplifies the computations by focusing directly on the surface data points themselves, applying calculations in a way that results in a streamlined and more efficient computational process. The results confirm the algorithm's impressive ability to deal with complex, curved surfaces efficiently. We added the new algorithm to the scalable scientific computing platform OpenFPM as open-source software, which makes it available for academics worldwide to use and allows it to run on supercomputers with few lines of code.
Alejandra Foggia, the co-author of the study, comments: “We compared our new method with the conventional ways of considering how surfaces are bumpy or uneven. Our new method is unique and can simulate faster, thus giving us better results. This renders it particularly useful for computational biology, helping us understand the complexities of biological surfaces.”
Ivo Sbalzarini concludes: “The idea behind this algorithm is elegantly simple but highly innovative. It represents a significant step forward in our ability to study complex biological phenomena on curved surfaces. This could pave the way for investigating the coupling between active mechanics and chemical processes on membranes and other biological surfaces.”
Abhinav Singh, Alejandra Foggia, Pietro Incardona & Ivo F. Sbalzarini: A Meshfree Collocation Scheme for Surface Differential Operators on Point Clouds. J Sci Comput 96, 89 (2023). https://doi.org/10.1007/s10915-023-02313-3