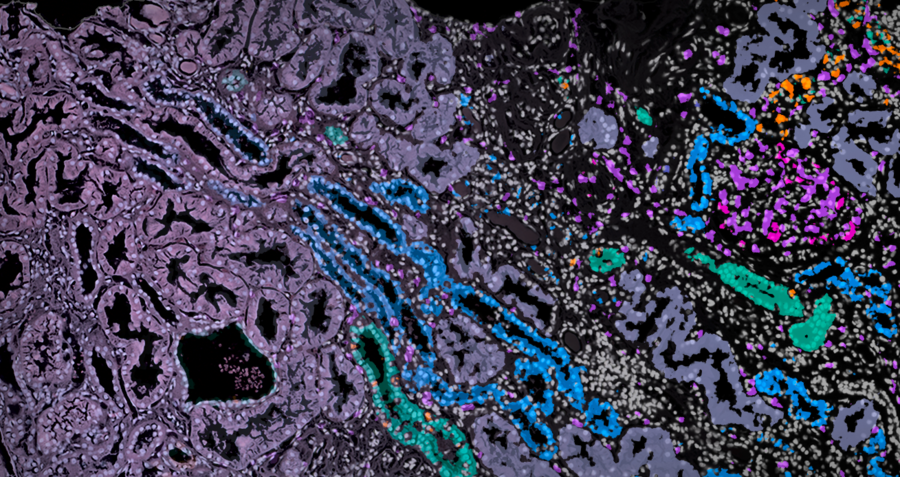
Mathematical methods reveal complex cell patterns in high-resolution kidney data © Katherine Benjamin/University of Oxford
Globally, kidney disease is forecast to be the 5th leading cause of death by 2040, and approximately 850 million people are living with chronic kidney disease. This disease is often due to autoimmune damage to the filtration units of the kidney, known as the glomeruli, which can occur in lupus, a disease that disproportionally affects women and people of non-white ethnicities, groups often underrepresented in research. Treatment options are limited, can have life-threatening side-effects, and often don’t slow the disease, which can then progress to an end stage, requiring dialysis or a kidney transplant.
There is an urgent need to develop safer, more effective, and personalized treatments for these kidney disorders. With mathematicians from Oxford, Heather Harrington, Professor of Mathematics at the TU Dresden and the University of Oxford and Director at the Max Planck Institute of Molecular Cell Biology and Genetics (MPI-CBG) in Dresden, Germany, and the Center for Systems Biology Dresden (CSBD), developed new mathematical approaches to quantify data from new experimental technologies.
Tools that allow scientists to understand gene expression in individual cells after separating them from a kidney sample have been around for about ten years, but very recently, new techniques are starting to reveal these cell signatures in a tissue context. This means the cells can be considered part of their local neighborhood, showing how cells move and signal to each other. This approach is exciting for autoimmune kidney diseases like lupus because the kidney is complex with more than 30 types of cells, and in lupus these are joined by multiple immune cell types, yet how these interactions lead to kidney damage is not well understood.
Aneesha Bhandari, supervised by Oxford Principal Investigator and Nephrologist Dr. Katherine Bull, has been using these new spatial methods to look at lupus kidney disease, but Katherine and Aneesha encountered a problem: the spatial information is at unprecedented subcellular resolution but very sparse and noisy, so deciding what type of cells they had found and where the boundary of each cell lies was challenging with these new methods. They knew there must be a way to dynamically use the local expression information to improve this, but how? Luckily, a conversation with mathematicians Professors Heather Harrington and Ulrike Tillmann and their student Katherine Benjamin revealed an elegant solution. Their research in topological data analysis identifies spatial patterns in data across different parameters. Together, the teams developed a new method, TopACT, to apply this mathematics to the spatial kidney data. They were able to reveal hidden patterns in the lupus kidney, with immune cells circling the glomerular regions. The approach turns out to work on a range of spatial platforms, which is important as these technologies are moving fast and could be applied in the future to 3-dimensional data.
Katherine Bull says, “This is a really interdisciplinary effort between mathematics and biology, allowing us to see granular detail and hidden patterns of inflammation in the kidney in lupus. These tools are an important step towards developing more targeted ways to treat this complex disease.”
Heather Harington says, “We are excited that this new spatial transcriptomics technology required us to develop novel mathematical approaches, building upon state-of-the-art topological data analysis. In this work, we identified spatial locations of sparse cells and then generated a hypothesis of a ring of immune cells in mouse kidney tissue, which was experimentally verified. Trying to understand this complex biological data offers interesting and challenging mathematical opportunities.”
Benjamin, K., Bhandari, A., Kepple, J.D. et al. Multiscale topology classifies cells in subcellular spatial transcriptomics. Nature (2024). https://doi.org/10.1038/s41586-024-07563-1