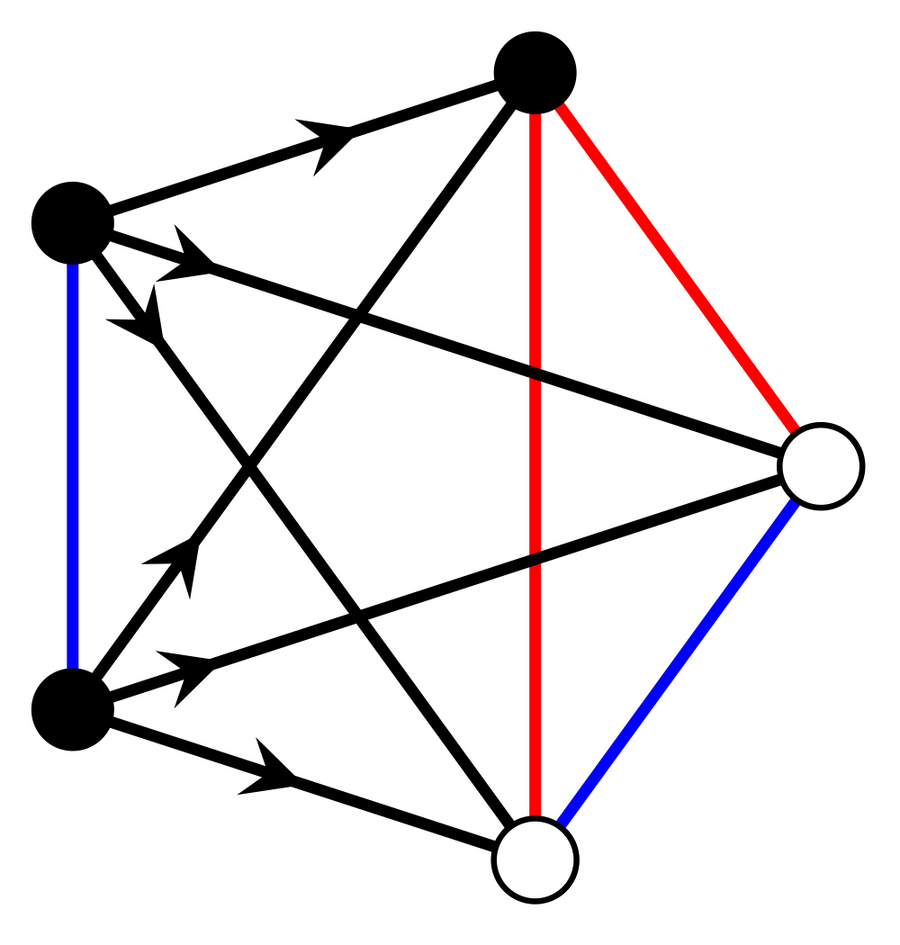
Beispiel für ökologische Wechselwirkungen zwischen fünf Arten, darunter konkurrierende (rot), mutualistische (blau) und Raubtier-Beute-Wechselwirkungen (schwarzer Pfeil). © Yu Meng et al., Cell Systems 2025
Welche allgemeinen Prinzipien bestimmen, ob Arten in einer ökologischen Lebensgemeinschaft stabil zusammenleben können? Diese Frage steht im Mittelpunkt der theoretischen Ökologie und der Theorie komplexer Systeme. Die Theorie der Zufallsmatrizen liefert allgemeine Muster dafür, wie Wechselwirkungen zwischen Arten – seien sie in einem Wettbewerbs-, Mutualismus- oder Räuber-Beute-Verhältnis – die Stabilität von Ökosystemen beeinflussen. Stabilität hängt jedoch auch von der Netzwerkanordnung dieser Wecheselwirkungen ab, das die Theorie der Zufallsmatrizen nicht vollständig abbilden kann.
Forschende des Max-Planck-Instituts für molekulare Zellbiologie und Genetik (MPI-CBG), des Max-Planck-Instituts für Physik komplexer Systeme (MPIPKS) und des Zentrums für Systembiologie Dresden (CSBD) haben einen neuen Ansatz entwickelt, um diese Fragen zu beantworten. Dabei stützen sie sich auf eine umfassende Analyse aller kleinen Netzwerke ökologischer Wechselwirkungen (mit bis zu fünf Arten). Yu Meng, Szabolcs Horvát, Carl Modes und Pierre Haas analysierten Hunderttausende von Netzwerken numerisch und stellten einen mathematischen Lehrsatz auf, der die Möglichkeit stabiler Koexistenz in einer Gemeinschaft mit ihren Untergemeinschaften verbindet. Die Autoren fanden heraus, dass selbst kleine Veränderungen im Netzwerk ökologischer Interaktionen die Möglichkeit stabiler Koexistenz erheblich beeinflussen.
„Wir haben auch festgestellt, dass ein sehr kleiner Aneil der Netzwerke Systeme bilden, die wir ‚unmögliche Ökosysteme‘ nennen, da Koexistenz in diesen Systemen schlichtweg unmöglich ist“, sagt Carl Modes.
„Unsere Studie zeigt, dass es tatsächlich die gesamte Struktur des Netwerks der Wechselwirkungen ist, die die Stabilität von Ökosystemen bestimmt. Unsere Ergebnisse können uns daher helfen, besser zu verstehen, wie Ökosysteme auf Umweltveränderungen reagieren werden“, fasst Pierre Haas zusammen.
Die Autoren arbeiten nun mit den Forschungsgruppen in Mathematik am MPI-CBG und am CSBD zusammen, um ihre numerischen Ansätze und Ergebnisse mit neuen mathematischen Werkzeugen auf größere ökologische Gemeinschaften auszuweiten.
Meng, Yu, Szabolcs Horvát, Carl D. Modes, and Pierre A. Haas. Impossible Ecologies: Interaction Networks and Stability of Coexistence in Ecological Communities. Cell Systems, June 2025, 101297. https://doi.org/10.1016/j.cels.2025.101297.